Ghi chú nhỏ bên lề - Tốn hàng tấn giấy mực đời sau
Vào năm 1637, Pierre de Fermat - một luật sư, nhà toán học nghiệp dư đã viết bên lề trống cuốn sách “Số Học” của Diophante rằng phương trình x^n + y^n = z^n không có nghiệm nguyên khác 0 của x, y ,z nếu n>2. Ông cũng không quên ghi chú thêm rằng “Quá hay, tôi đã chứng minh được điều này nhưng lề sách không còn đủ chỗ để viết”. Những dòng này được người ta phát hiện ra sau khi ông mất 30 năm và Fermat đâu biết rằng, ông đã ghi lại một đề bài quá khó, tốn công sức của biết bao nhiêu nhà toán học trong suốt 358 năm, mãi đến khi nó được chứng minh bởi Andrew Wiles vào năm 1995. Định lý Fermat trở thành một định lý cực kì nổi tiếng bởi hành trình chứng minh nó cũng như hoàn cảnh ra đời. Không ít lần, đây được xem là vấn đề khó khăn nhất của trí khôn nhân loại.![[IMG]](https://photo2.tinhte.vn/data/attachment-files/2021/02/5365798_fermat-last-theorem-4.jpg)
Một trang sách của cuốn Arithmetica ấn bản năm 1670, tác giả Diophante - Nơi Fermat ghi chú lại định lý của mình cùng câu nói thách thức bao nhiêu cái đầu vĩ đại
Tiểu sử của Fermat
Pierre de Fermat sinh ngày 17/8/1601 tại miền Tây Nam nước Pháp trong một gia đình giàu có với người Cha là một thương nhân buôn bán da. Mặc dù được hậu thế biết đến như một nhà toán học, nhưng xuất phát điểm của Fermat là một luật sư. Ông học luật tại đại học Orléan năm 1623 và nhận được bằng cử nhân luật năm 1626. Fermat có niềm say mê bất tận với toán học. Ông thường xuyên tự học hỏi về toán và nghiên cứu nhiều về các công trình toán học. Vì tình yêu với toán, người đời sau này gán cho Fermat cái tên “Hoàng tử của những người nghiệp dư”.
Fermat là người học cao, hiểu rộng và có một kho tàng kiến thức rất lớn, đặc biệt là về toán học. Bản thân ông có thể sử dụng thông thạo 6 ngôn ngữ như tiếng Pháp mẹ đẻ, tiếng Latin, tiếng Hy Lạp cổ, Ý, Tây Ban Nha và tiếng Occitan. Quay trở lại với toán, những công trình của ông thường nằm dưới dạng thư tay viết cho những người bạn để trao đổi. Fermat cũng nêu nhiều định lý, nhưng có khá ít những chứng minh của ông về các định lý này. Các nhà khoa học hiện đại cho biết, ông thậm chí còn đưa ra rất nhiều ý tưởng ban đầu về phép vi tích phân trước khi nó được Newton và Leibniz độc lập tìm ra sau này.

Ông mất ngày 12/1/1665 tại Castres, tên của ông được đặt cho một trường Trung học cổ và uy tín nhất Toulouse là Lycée Pierre-de-Fermat. Người hậu thế sau này thường biết đến ông thông qua hai định lý Fermat. Đó là định lý nhỏ Fermat có dạng a^p ≡ a(mod p). Định lý này dễ chứng minh được, tuy nhiên cái còn lại thì không dễ như thế, đó là định lý lớn của Fermat, hay còn được gọi là định lý cuối cùng của Fermat mà mình đã nêu bên trên.
Định lý lớn của Fermat
Mọi thứ bắt nguồn từ định lý Pythagore mà tất cả chúng ta đều đã từng học qua vào năm cấp 2. Phương trình của định lý Pythagore có dạng x^2 + y^2 = z^2, bộ những nghiệm x, y, z thoả phương trình trên được xem là một bộ số Pythagore, lấy ví dụ (3,4,5) hoặc (5,12,13). Từ hàng ngàn năm trước, khoảng năm 1500 trước công nguyên, người Babylon đã tìm được bộ ba (4961,6480,8161), bộ ba này được xem là rất khó để tính vào thời điểm đó vì thiếu những công cụ hỗ trợ tính toán. Mở rộng và thay đổi từ phương trình Pythagore, Fermat đã phát biểu:“Không tồn tại nghiệm nguyên khác 0 của x, y, z nếu n>2 của phương trình x^n + y^n = z^n”
Chỉ một phát biểu ngắn gọn như thế đã làm cho rất nhiều người lao đầu vào tìm cách giải. Câu khẳng định đã tìm được cách giải của Fermat như làm cho người khác có thêm niềm tin rằng định lý này đúng, ngày càng nhiều các nhà toán học muốn giải quyết nó nhưng đều thất bại. Nhiều tài liệu còn ghi lại, có những người đã phải tự tử vì quá stress khi cố giải bài toán này. Nhìn chung, tất cả những nỗ lực chứng minh định lý lớn Fermat lúc bấy giờ đều đi vào ngõ cụt.
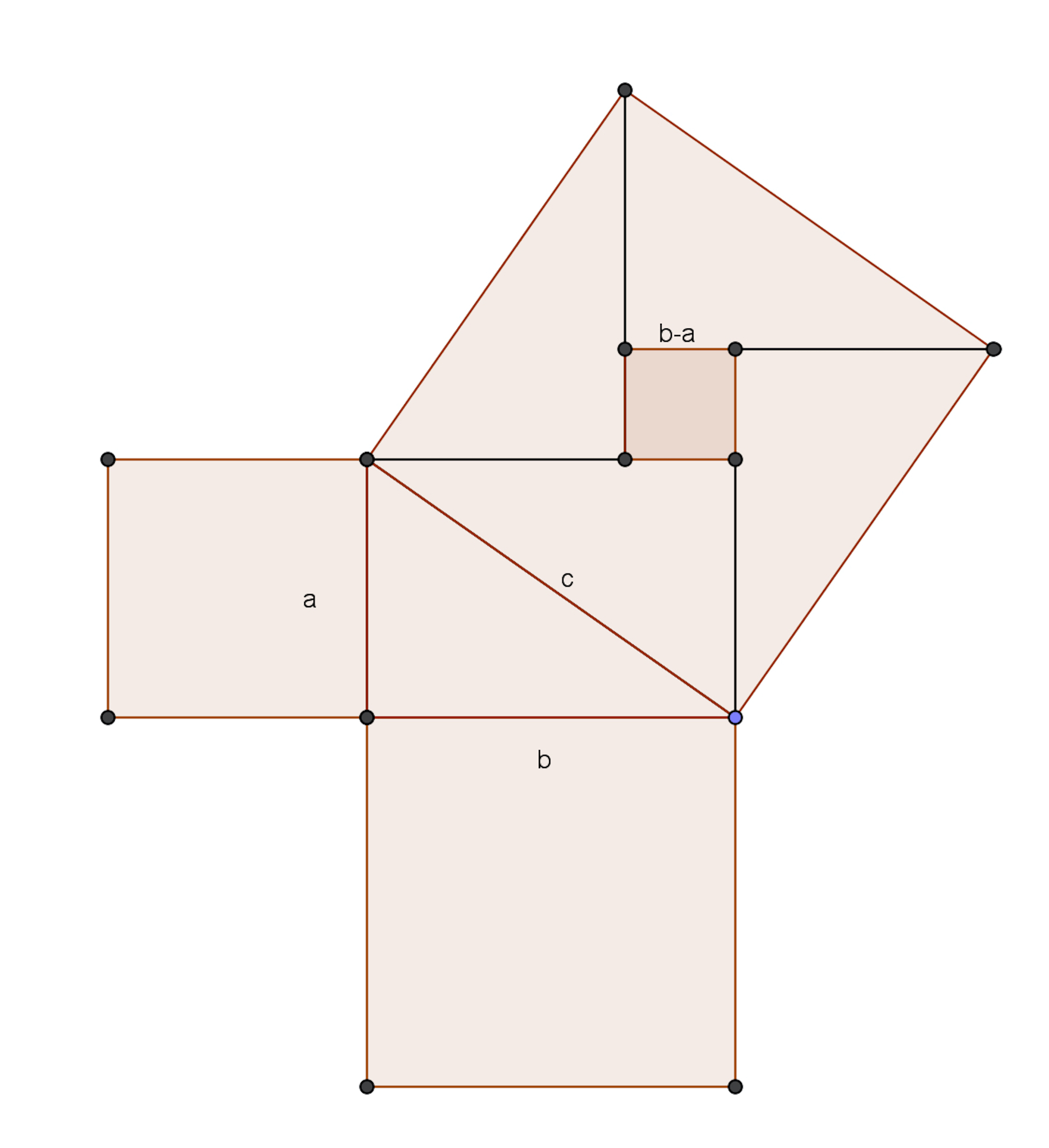
Biểu đạt hình học của định lý Pythagore, một trường hợp của định lý Fermat với n = 2
Không có bất kì tín hiệu nào cho thấy việc chứng minh dạng tổng quát sẽ thành công, các nhà toán học bắt đầu chứng minh định lý trên với một vài trường hợp n cụ thể. Năm 1753, nhà toán học Euler đã chứng minh định lý lớn Fermat với trường hợp n = 3, hay viết tắt là (FLT)3. Sau đó ông tiếp tục chứng minh (FLT)4, bản thân Fermat cũng đã chứng minh được (FTL)4. Sau đó vào năm 1828, Dirichlet chứng minh được (FLT)5 và 12 năm sau, Gabriel Lame đã chứng minh được với n=7. Như vậy phải mất tới 200 năm, con người mới có thể chứng minh định lý Fermat lớn đúng với các n = 3, 4, 5, 6, 7. Cuộc hành trình chứng minh định lý Fermat bắt đầu khởi sắc sau khi nhà toán học người Đức là Ernst Kummer đã chứng minh được định lý này đúng với n là các số nguyên tố nhỏ hơn 100, trừ số 37, 59 và 67 là những số nguyên tố phi chính quy.
Quảng cáo
Để chứng minh dạng tổng quát với mọi n là quá khó. Có người thậm chí còn cho rằng nền văn minh của con người sẽ sụp đổ trước khi bài toán này được giải quyết. Việc chứng minh định lý Fermat dần bị lãng quên. Sau này định lý Fermat còn được đưa vào sách kỷ lục Guinness với danh hiệu “Vấn đề toán học khó nhất mọi thời đại”.
Giải thưởng danh giá giành cho người chứng minh được định lý lớn của Fermat
Đây là giải thưởng do một nhà toán học người Đức tên là Paul Wolfskehl thành lập. Nhân vật này từng học y khoa tại đại học Leipzig và sau đó đợc nhận bằng tiến sĩ tại Đại học Heidelberg. Tuy nhiên không may cho ông rằng mình mắc phải chứng bệnh đa xơ cứng và buộc phải theo đuổi một con đường khác vì vấn đề sức khoẻ. Trong giai đoạn từ năm 1880 đến năm 1883, ông học toán tại đại học Bonn và đại học Bern, sau đó nhận bằng tiến sĩ toán học.Có nhiều giai thoại để kể về nguồn gốc của giải thưởng Wolfskehl giành cho những ai giải được định lý Fermat, nhưng nổi tiếng nhất vẫn là câu chuyện về cuộc tự sát bất thành của ông. Năm 1908, Wolfskehl gặp những rắc rối liên quan đến đời sống riêng tư. Quá chán nản vì những bất hạnh mà mình gặp phải, ông dự định sẽ tự sát vào lúc giữa đêm để kết thúc sự đau khổ. Chẳng biết là may mắn hay xui xẻo, trong lúc chờ đợi đến giờ G, Wolfskehl vô tình đọc được chứng minh của Kummer về định lý của Fermat. Sự ham mê nghiên cứu toán học của ông trỗi dậy và Wolfskehl suy tư về nó mãi cho đến khi quên mất kế hoạch tự sát của mình. Từ đó, ông không nghĩ đến cái chết nữa và quyết tâm dành hết toàn bộ tài sản mà mình có để thành lập giải thưởng Wolfskehl.
Theo đó, giải thưởng mang tên ông sẽ được trao cho bất kì ai chứng minh được thành công định lý cuối của Fermat dạng tổng quát với mọi n. Tổng trị giá giải thưởng là 100.000 mác, tương đương 1.75 triệu đô la Mỹ lúc bấy giờ và dĩ nhiên với số tiền này, giải Wolfskehl thậm chí còn lớn hơn cả giải Nobel (và giải Nobel cũng không có giải trao cho thành tựu toán học). Ở thời điểm giải thưởng Wolfskehl bắt đầu được thông báo tới mọi người, nỗ lực chứng minh định lý Fermat bắt đầu “nóng” trở lại. Theo những tài liệu lịch sử, chỉ tính trong năm mà giải thưởng được công bố, có hơn 600 bài chứng minh được gửi về và những năm sau đó, con số này tiếp tục được tăng cao. Đáng buồn thay, toàn bộ những xấp tài liệu chứng minh đó, ĐỀU KHÔNG ĐÚNG.
Cuối cùng, vào năm 1997, giải thưởng Wolfskehl được trao cho giáo sư Andrew John Wiles sau hàng năm nỗ lực để giải quyết vấn đề mà Fermat để lại chỉ trong lề của một cuốn sách.
Taniyama-Shimura: Chìa khoá để giải quyết vấn đề hàng thế kỉ
Rất nhiều nỗ lực chứng minh định lý cuối cùng của Fermat mặc dù sai, song, chúng không hoàn toàn vô nghĩa. Mặc khác có những thứ lại tạo ra tiền đề cho chiến thắng của Andrew Wiles, và đó chính là giả thuyết Taniyama-Shimura. Giải thích định lý này có lẽ khả năng của mình chưa đủ sức, và thậm chí có viết thêm 10 bài nữa thì số lượng anh em đọc hiểu được chắc chỉ đếm trên đầu ngón tay nên mình sẽ chỉ giới thiệu qua về nó.Quảng cáo
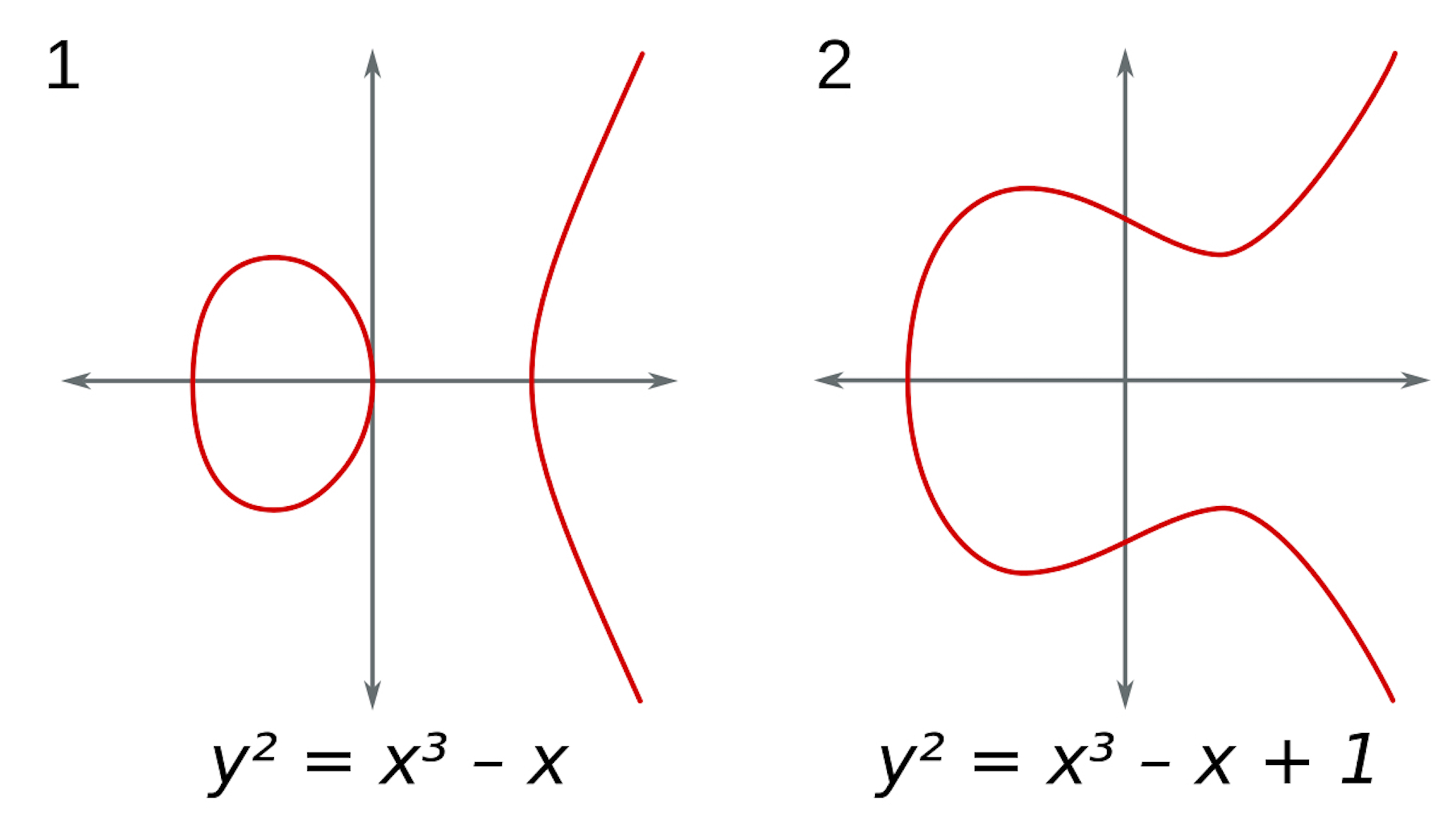
Đại khái thì định lý Taniyama-Shimura thể hiện mối quan hệ giữa đường cong elip và các dạng modular của lý thuyết số. Định lý này được hai nhà toán học người nhật là Yataka Taniyama và Goro Shimura nghiên cứu vào khoảng năm 1955, họ đã phát biểu rằng mỗi phương trình elip đều gắn liền với một dạng modular. Với giả thuyết Taniyama-Shimura (gọi là giả thuyết vì lúc bấy giờ, nó vẫn chưa được chính minh thành công), nó đã nối giúp hai lĩnh vực rất quan trọng trong toán học là topo và lý thuyết số trở nên liên hệ với nhau. Ban đầu khi được nghiên cứu, định lý này gần như không có bất kì một mối liên hệ nào đến định lý lớn Fermat, cho đến khi Gerhard Frey chỉ ra mối liên hệ như thế bằng cách biến đổi phương trình của Fermat thành một phương trình elliptic. Tất cả những bước trên để cuối cùng đúc ra một kết luận, nếu giả thuyết Taniyama-Shimura được chứng minh là đúng, thì định lý của Fermat cũng sẽ đúng. Tuy nhiên việc chứng minh định lý Taniyama-Shimura là hết sức khó khăn, không thua kém gì định lý Fermat.
Sir Andrew Wiles và phát súng tuyên bố kết thúc vấn đề toán học tồn tại 358 năm
Thông tin về mối quan hệ giữa định lý Taniyama-Shimura và định lý Fermat đến tai của Andrew Wiles, lúc này đang là giáo sư người Anh giảng dạy tại đại học Princeton nước Mỹ. Nhận ra tính then chốt của việc chứng minh giả thuyết Taniyama-Shimura, ông đã tập trung để thực hiện điều này trước khi công bố thành công lần đầu tiên sau 7 năm trời ròng rã.
Andrew Wiles chụp cạnh định lý lớn Fermat đang được ông ghi lên bảng
Vào một ngày tháng 6 năm 1993, Andrew Wiles có buổi thuyết trình tại đại học Cambridge trong một hội thảo về lý thuyết số. Bài thuyết trình được chia thành 3 buổi, và đến cuối buổi thứ ba, sau khi ông hoàn thành những dòng chứng minh cuối cùng của giả thuyết Taniyama-Shimura, Andrew Wiles nhẹ nhàng nói:
“Vậy là có lẽ tôi vừa chứng minh được định lý lớn Fermat rồi đấy!”
Wiles sau đó gửi tất cả bài báo cáo của mình lên mội hội đồng phản biện gồm 6 chuyên gia ngay sau khi kết thúc buổi thuyết trình cuối cùng. Tất cả chuyên gia chịu trách nhiệm dò lại công trình của Andrew Wiles đều phải kĩ lưỡng kiểm tra từng dòng, từng ký hiệu toán học, từng phép biến đổi trong một bản thảo dài 200 trang. Song, đến cuối cùng người ta lại nhận thấy trong bài nghiên cứu của ông có một lỗi sai hết sức căn bản, thế là lần công bố đầu tiên của Wiles đã thất bại.

Richard Taylor, học trò của Andrew Wiles tại đại học Cambridge - Người đã giúp thầy của mình chứng minh thành công định lý Taniyama-Shimura
Tuy nhiên ông không hề nản chí mà dừng nghiên cứu, đổi lại Wiles tiếp tục tìm cách chữa lỗi sai, nghiên cứu lại cùng với Richard Taylor, một học trò của ông. Giữa một rừng chữ và số, hai người gần như đã bỏ cuộc cho đến khi Wiles và Taylor bắt đầu nhận ra một hướng đi sáng vào tháng 9 năm 1994. Cả hai bắt đầu khai thác điểm này và nửa năm sau, vào tháng 3 năm 1995, Wiles lại một lần nữa công bố chứng minh của mình về định lý Fermat. Nhờ giải được định lý Taniyama-Shimura, ông đã có thể chứng minh định lý Fermat cuối cùng, và lần này không có bất kì sai lầm nào được phát hiện. Andrew Wiles đã khép lại 358 năm tìm cách chứng minh bài toán này. Định lý Taniyama-Shimura sau này còn được gọi là định lý Taniyama-Shimura-Wiles, để ghi ơn công sức chứng minh của Andrew Wiles trong nỗ lực bền bỉ của mình.

Andrew Wiles trong lễ trao giải thưởng
Andrew Wiles được nhận giải thưởng Wolfskehl vào năm 1997, ông cũng được phong tước hiệp sĩ bởi Nữ Hoàng Anh và hơn hết, ông được người đời ca tụng vì đã giải được bài toán quá khó trong lịch sử loài người. Về phần Fermat, người ta liên tục đặt ra câu hỏi liệu ông có thực sự chứng minh được định lý này hay không? Tuy nhiên câu hỏi đó có lẽ chẳng ai có thể trả lời được. Nếu thực sự ông có thể chứng minh như các mà ông đã viết, thì chúng ta phải thực sự ca tụng nhà toán học nghiệp dư này. Dù như như thế nào chăng nữa, định lý Fermat và công cuộc giải được nó đã làm cho toán học trở nên thú vị hơn, nhiều lời giải mặc dù sai những vẫn đóng góp được nhiều thứ cho toán học và giúp con người tiến bộ hơn.
Tham khảo (1), (2), (3), (4), (5), (6), (7), (8)


