Các tổng vô hạn bộc lộ tính thống nhất của toán học như thế nào?

Các tổng vô hạn (infinite sums) nằm trong số những khái niệm mạnh mẽ nhưng lại bị đánh giá thấp nhất trong toán học, chúng có khả năng nối kết các khái niệm trên mạng lưới rộng lớn của toán học.

Gạch nối giữa các lãnh vực toán học

Khi nói về sự xuất sắc tuyệt đối, thật khó để đánh bại John von Neumann (1903-57). Ông là một kiến trúc sư của máy tính hiện đại đồng thời là nhà phát minh ra lý thuyết trò chơi (game theory), và trên hết, von Neumann đã trở thành một huyền thoại vì khả năng tính nhẩm nhanh như chớp của mình. Khi là một cậu bé 6 tuổi, Neumann đã có thể nhân và chia tám chữ số trong đầu mình, điều mà nếu chúng ta tự làm bằng tay có thể mất đến vài tiếng hay cả ngày.
Chuyện kể rằng một ngày nọ, có người thách thức ông bằng một câu đố. Câu đố như sau: Hai người đi xe đạp bắt đầu chạy ở hai đầu đối diện của một con đường dài 20 dặm. Mỗi người đạp xe về phía người kia với tốc độ 10 dặm một giờ. Khi họ bắt đầu đi, một con ruồi đậu trên bánh trước của một trong hai chiếc xe cũng bắt đầu bay và bay với tốc độ 15 dặm một giờ về phía chiếc xe đạp kia (đây là điều kiện lý tưởng khi chúng ta giả định con ruồi bay thẳng, đều đặn). Ngay khi đến đó, nó lập tức quay vòng lại và lao ngược về phía chiếc xe đạp đầu tiên, sau đó quay lại chiếc thứ hai, và cứ tiếp tục như vậy. Nó tiếp tục bay tới bay lui cho tới khi cuối cùng nó bị kẹt giữa lốp xe trước của chúng khi hai xe đạp va chạm. Hỏi tổng cộng con ruồi đã bay được bao xa trước khi nó bị bóp nát?
Nghe có vẻ khó nhằn. Hành trình bay tới bay lui của con ruồi bao gồm vô số phần, mà mỗi phần ngắn hơn phần trước nó. Việc cộng hết chúng vào có vẻ như là một nhiệm vụ dễ gây nản lòng.

John von Neumann đứng bên cạnh máy tính lưu trữ chương trình tại Viện Nghiên cứu Tiên tiến (IAS), Princeton, New Jersey, năm 1945. Ảnh: Guardian.

Nhưng vấn đề lại trở nên dễ dàng nếu bạn nghĩ về những người đi xe đạp chứ không phải con ruồi. Trên một con đường dài 20 dặm, hai người đạp xe tiến gần về nhau với vận tốc 10 dặm một giờ sẽ gặp nhau ở giữa sau 1 giờ (vì hiển nhiên là mỗi người đi được 10 dặm sau 1 giờ). Và trong 1 giờ đó, bất kể con ruồi bay theo đường nào, nó phải đi được 15 dặm, vì nó đang bay 15 dặm một giờ.

Khi von Neumann nghe thấy câu đố, ông lập tức trả lời: “15 dặm.” Người hỏi đầy thất vọng nói, "Ồ, anh đã thấy mánh khóe ở đây." “Mánh khóe gì?” von Neumann đáp ngay. “Tôi chỉ cộng lại hết chuỗi vô hạn.”
Chuỗi vô hạn - tổng của nhiều vô tận các con số, biến số hoặc hàm số mà chúng tuân theo một quy tắc nhất định - là những tay chơi thứ yếu trong tấn kịch vĩ đại của môn giải tích. Trong khi các phép tính đạo hàm và tích phân chiếm lấy sân khấu một cách chính đáng, thì chuỗi vô hạn khiêm tốn đứng sang một bên. Khi chúng xuất hiện thì đó là lúc gần kết thúc cuộc đua, khi mọi người đang cố gắng chạy qua vạch đích.

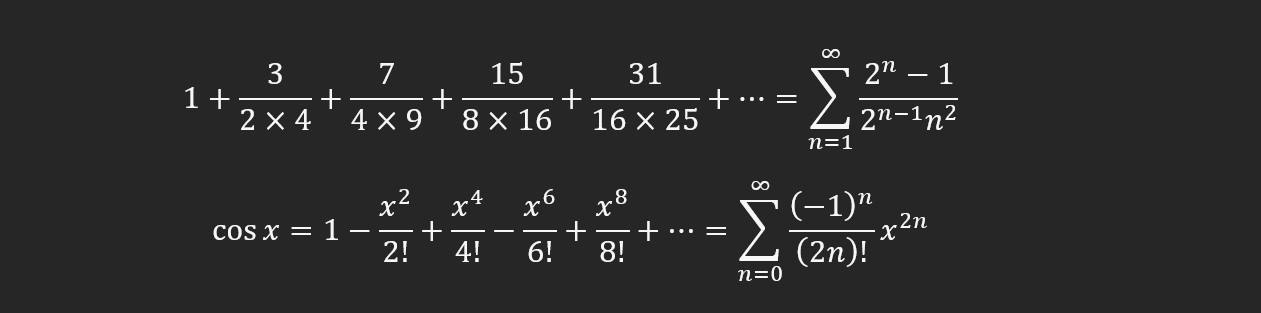
Ví dụ về chuỗi vô hạn của các số thuần túy (chuỗi trên), và chuỗi vô hạn của các hàm số (chuỗi dưới) dùng để tính hàm cosine theo cách thủ công. Các công thức sau dấu sigma (∑) được gọi là một chỉ lệnh hay toa thuốc (prescription) giúp chúng ta biết được cách tính của từng số hạng trong tổng vô hạn, đó là quy tắc của chúng. Dấu chấm than (!) là phép tính giai thừa, ví dụ: 4! = 1 x 2 x 3 x 4.

Vậy tại sao chúng ta phải nghiên cứu chúng? Chuỗi vô hạn rất hữu ích để tìm các giải pháp gần đúng cho những vấn đề khó khăn và để minh họa các điểm tinh tế trong tính chặt chẽ toán học. Nhưng trừ khi bạn là một nhà khoa học đầy tham vọng, thì đó chỉ là một cái ngáp dài vì quy trình tìm ra chúng rất tẻ nhạt. Ngoài ra, chuỗi vô hạn thường được trình bày mà không có bất kỳ ứng dụng nào trong thế giới thực. Một số ít xuất hiện — niên kim, các khoản thế chấp, thiết kế phác đồ hóa trị — lại có vẻ xa vời đối với đại đa số chúng ta.
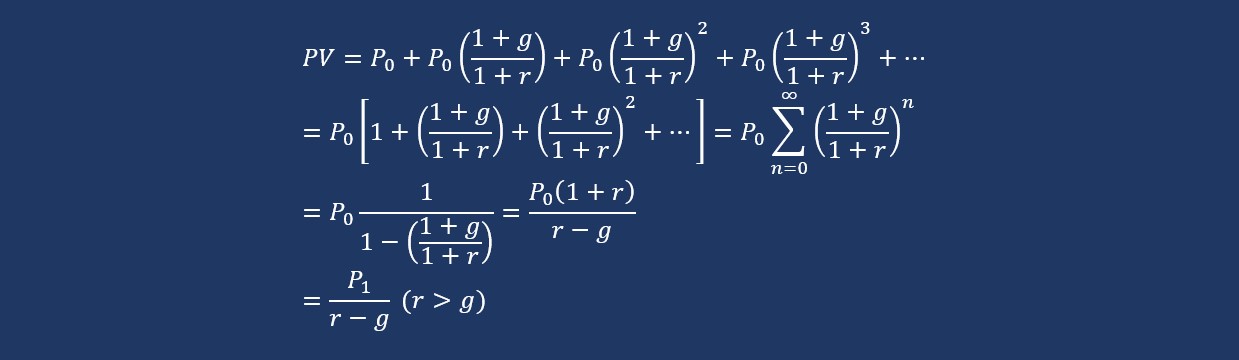Sự xuất hiện của chuỗi vô hạn trong một niên kim được giả định là kéo dài vô thời hạn, gia tăng với tỷ lệ g và chiết khấu bằng lãi suất r hằng năm. Công thức này thường gọi là Gordon dùng để định giá cổ phiếu hoặc trong các trường hợp phức tạp hơn, quy tắc này dùng để xác định giá trị công ty, tỷ suất r thường được gọi là chi phí vốn mà nhà đầu tư đòi hỏi. Mặc dù dòng tiền kéo dài vô hạn nhưng giá trị hiện tại của chúng luôn là một con số nhất định, đây là tính hội tụ của một chuỗi vô hạn.

Lý do thuyết phục nhất để tìm hiểu về chuỗi vô hạn là chúng là những vật nối kết tuyệt vời. Chúng tiết lộ mối liên hệ giữa các lĩnh vực toán học khác nhau, hé lộ những liên kết bất ngờ giữa mọi thứ xuất hiện trước đó. Chỉ khi chúng ta học đến phần nói về chuỗi vô hạn của môn giải tích thì cấu trúc thực sự của toán học - toàn bộ toán học - cuối cùng mới bắt đầu nổi lên rõ rệt.

Bài toán của người bán nón

Trước khi đi vào giải thích điều này, ta hãy cùng xem một câu đố khác liên quan đến chuỗi vô hạn. Việc từng bước giải quyết vấn đề này sẽ làm rõ cách von Neumann giải vấn đề con ruồi, và nó sẽ tạo tiền đề cho việc suy nghĩ về chuỗi vô hạn một cách bao quát hơn.
Giả sử bạn muốn mua một cái nón lạ mắt từ một người bán hàng rong. Anh ta chào bán với giá 24 đô la. “Còn 12 đô thì sao?” bạn trả giá. “Vậy hãy chia đôi phần chênh lệch,” anh ta trả lời, “18 đô la.” Nghĩa là lấy trung bình cộng giữa 12 và 24 đô la.
Thường thì chuyện mua nón đến đây là xong. Chia phần chênh lệch có vẻ hợp lý, nhưng không phải đối với bạn, bởi vì bạn đã đọc cùng một cuốn sách hướng dẫn đàm phán như người bán, mang tên “Nghệ thuật Mặc cả Vô hạn” (The Art of Infinite Haggling). Bạn phản đối bằng cách tự mình đề nghị chia đôi tiếp phần chênh lệch, ngoại trừ hiện tại nó nằm trong khoảng từ 12 đô la đến con số mới nhất vừa đạt được, 18 đô la. “Vậy thì sao?” bạn nói, "15 đô la và chuyện này coi như xong." Người bán hàng lại nói: “Ồ không, bạn tôi, ta hãy chia lại phần chênh lệch, 16.5 đô la." (trung bình cộng của 15 và 18). Việc này tiếp tục đi theo chiều hướng ngớ ngẩn cho tới khi cả hai hội tụ về cùng một mức giá. Cái giá cuối cùng đó là gì?
Câu trả lời là tổng của một chuỗi vô hạn. Để xem coi đó là bao nhiêu, ta quan sát thấy các đề nghị liên tiếp tuân theo một khuôn mẫu có trật tự:
24 giá chào bán của người bán rong
12 = 24 – 12 đề nghị đầu tiên của bạn

18 = 24 – 12 + 6 chia đôi phần chênh lệch giữa 12 và 24 (người bán)
15 = 24 – 12 + 6 – 3 chia đôi phần chênh lệch giữa 12 và 18 (bạn)
16.5 = 24 – 12 + 6 – 3 + 1.5 chia đôi phần chênh lệch giữa 15 và 18 (người bán)
15.75 = 24 – 12 + 6 – 3 + 1.5 – 0.75 chia đôi phần chênh lệch giữa 16.5 và 15 (bạn)
Điều quan trọng là các số ở phía bên trái của dấu bằng được xây dựng một cách có hệ thống từ chuỗi số ngày càng dài ra ở bên phải. Với mỗi số xuất hiện trong dãy (24, −12, 6, −3, 1.5, –0.75, …) bằng một nửa số liền trước nó nhưng trái dấu. Vì vậy khi đi dần đến giới hạn, mức giá P mà bạn và nhà cung cấp sẽ đồng ý là
P = 24 – 12 + 6 – 3 + 1.5 – 0.75 + …, trong đó ba dấu chấm có nghĩa là chuỗi kéo dài đến vô tận.
Thay vì gắng sức tập trung vào một biểu thức dài vô hạn như vậy, chúng ta có thể thực hiện một thủ thuật khéo léo để làm cho vấn đề trở nên dễ dàng. Nó cho phép chúng ta triệt bỏ đi tập hợp các số hạng vô tận đến khó hiểu đó, để lại cho chúng ta một thứ đơn giản hơn nhiều để tính toán.
Cụ thể là, hãy nhân đôi P. Việc làm này cũng sẽ nhân đôi tất cả các số ở bên phải. Như vậy,
2P = 48 – 24 + 12 – 6 + 3 – 1.5 + …
Điều này giúp ích như thế nào? Ta quan sát thấy chuỗi vô hạn các số hạng trong 2P gần giống như nó trong chính P, ngoại trừ việc chúng ta có một con số bắt đầu mới (48) và tất cả các dấu cộng và dấu trừ cho các số ban đầu của chúng ta đều bị đảo ngược. Vì vậy, nếu chúng ta cộng chuỗi tính P vào chuỗi tính 2P (cộng vế theo vế) thì các số 24 và 12 và mọi thứ khác sẽ bị triệt tiêu theo cặp, ngoại trừ số 48, không có số đối ứng để triệt bỏ nó, dĩ nhiên người bán rong chắc phải rất mừng vì nó vẫn còn đó. Vậy 2P + P = 48, nghĩa là 3P = 48 và do đó P = 16 đô la.
Đó là số tiền bạn phải trả cho cái nón sau khi mặc cả không hồi kết.

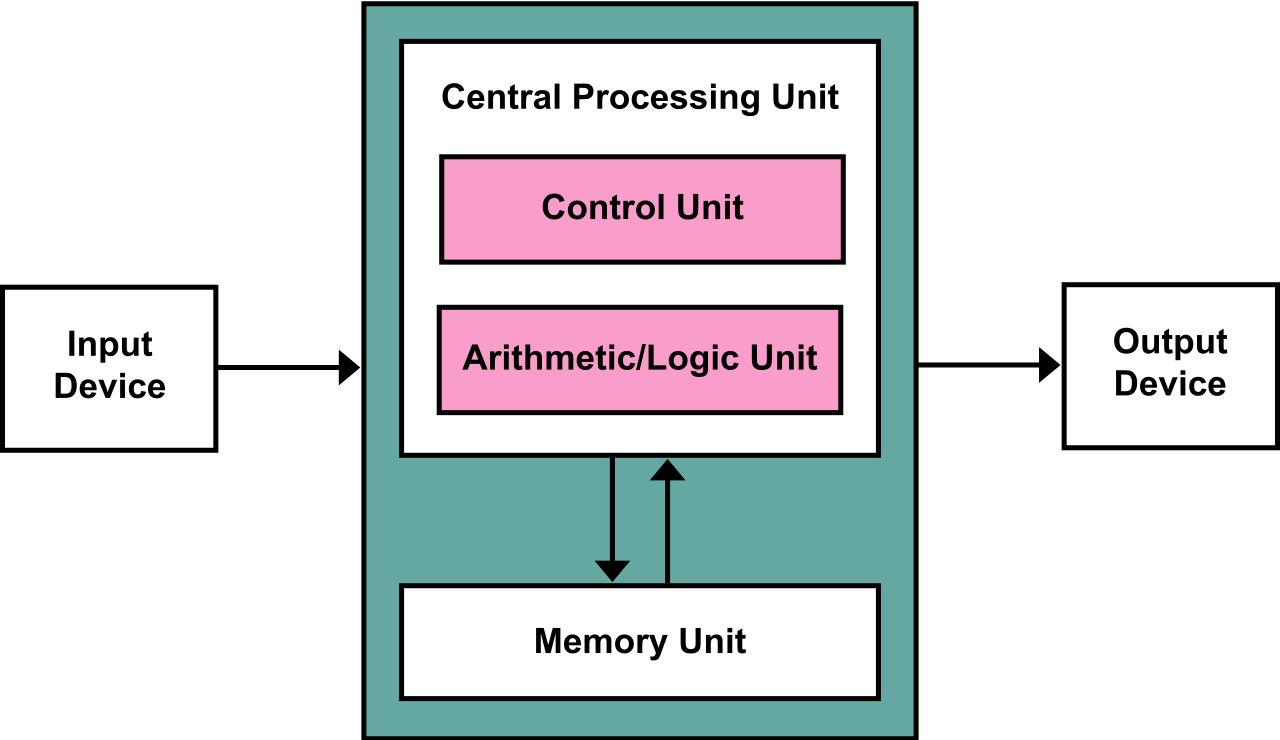
Kiến trúc máy tính theo miêu tả của Newmann năm 1945, nó bao gồm đơn vị xử lý chứa một đơn vị xử lý số học và đơn vị kiểm soát, bộ nhớ lưu trữ dữ liệu và các chỉ lệnh (instruction), các cơ chế đầu ra/đầu vào. Tên gọi của đơn vị xử lý logic số học (ALU) đã thể hiện bản chất của máy tính, đối với các hàm siêu việt như hàm lượng giác hay hàm số mũ, nó không thể hiểu về các hàm đó theo cách thức trừu tượng mà con người hiểu. Nó chỉ có thể hiểu theo nghĩa “số học”, nghĩa là các hàm này phải được con người diễn giải theo cách của những phép tính số học sơ đẳng (cộng, trừ, nhân, chia) để nó có thể tính được. Vì vậy khi máy tính giải quyết các hàm này, nó sẽ áp dụng các chuỗi vô hạn tương ứng để tính. Ảnh: Wikipedia.

Quay về bài toán hai chiếc xe đạp

Bài toán về con ruồi và hai chiếc xe đạp cũng tuân theo dạng toán tương tự. Với một chút nỗ lực, bạn có thể suy ra rằng mỗi chặng bay tới bay lui của con ruồi dài bằng 1/5 chặng đường trước đó. Von Neumann hẳn sẽ coi đó là trò trẻ con khi tính tổng “chuỗi hình học”, loại chuỗi đặc biệt mà chúng ta đang xem xét, trong đó tất cả các số hạng liên tiếp nhau đều có cùng một công bội. Đối với bài toán con ruồi, công bội đó là 1/5. Còn đối với vấn đề trả giá nón, công bội là –0.5.
Nhìn chung, bất kỳ chuỗi hình học S nào cũng có dạng
S = a + ar + ar² + ar³ + …
trong đó r là công bội và a là một số gọi là số hạng đầu tiên. Nếu công bội r nằm giữa –1 và 1, như trong hai vấn đề của chúng ta, thì thủ thuật được sử dụng ở trên có thể được điều chỉnh bằng cách nhân không phải với 2 mà với r, rồi trừ vế theo vế để chỉ ra rằng tổng của chuỗi là:
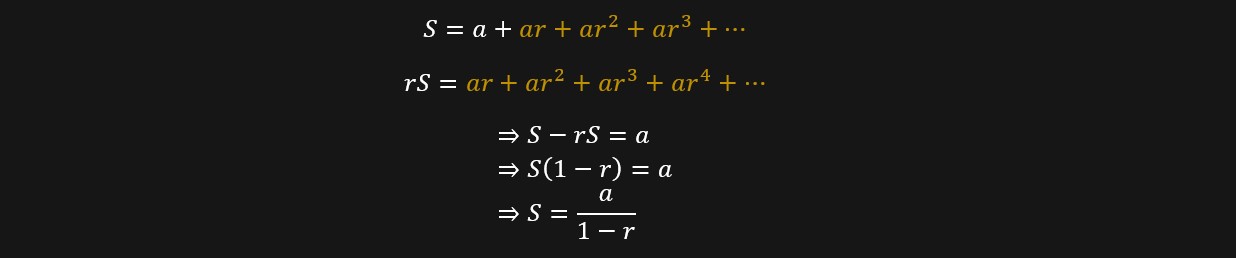Cụ thể thì đối với vấn đề trả giá nón, a là 24 đô la và r là –0.5. Thế những số đó vào công thức cho chúng ta S = 24/(1 + 0.5) = 16 đô la, như đã thấy.
Đối với bài toán con ruồi, chúng ta phải làm việc một chút để tìm ra số hạng đứng đầu, a. Đó là quãng đường mà con ruồi đi được trên chặng đầu tiên của hành trình bay đi bay về, vì vậy để tính toán nó chúng ta phải tìm ra vị trí đầu tiên mà con ruồi đang di chuyển với vận tốc 15 dặm một giờ gặp chiếc xe đạp đang lao tới nó với vận tốc 10 dặm một giờ. Vì vận tốc của chúng cân xứng nhau theo tỷ lệ 15:10 hay 3:2 nên chúng gặp nhau khi con ruồi đã đi được 3/(3 + 2) của quãng cách 20 dặm, điều này cho ta biết a = 3/5 x 20 = 12 dặm. Lập luận tương tự tiết lộ rằng các chặng giảm đi theo công bội là r = 1/5 mỗi lần con ruồi quay đầu lại. Von Neumann đã thấy được toàn bộ việc này ngay tức thì và bằng cách dùng công thức a/(1 – r) ở trên ông đã tìm ra tổng quãng đường con ruồi đi được:

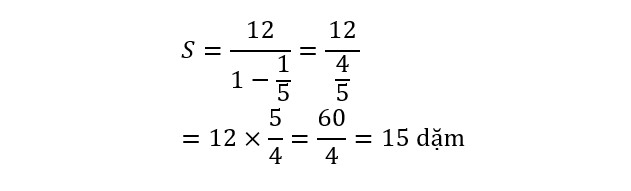
Những người họ hàng bí mật

Bây giờ hãy quay lại vấn đề lớn hơn: Làm cách nào để các chuỗi như thế này phục vụ cho việc nối kết những phần khác nhau của toán học? Để thấy được điều này, chúng ta cần mở rộng quan điểm của mình về các công thức như
1 + r + r² + r³ + … = 1/(1 – r),
mà là cùng một công thức như trước đó với a bằng 1. Thay vì nghĩ về r như một con số cụ thể như 1/5 hay –½, ta hãy nghĩ về r như một biến. Khi đó phương trình nói lên điều gì đó thú vị; nó biểu thị một loại thuật giả kim toán học, như thể chì có thể được hóa thành vàng. Nó xác quyết rằng một hàm số cho trước theo biến r (ở đây là 1 chia cho 1 – r) có thể được hóa thành thứ gì đó sơ đẳng hơn, một sự kết hợp của các lũy thừa đơn giản của r, chẳng hạn r² và r³ và cứ tiếp tục như vậy.
Điều tuyệt vời là điều này cũng đúng với vô số hàm số khác xuất hiện hầu như ở mọi ngõ ngách trong khoa học và kỹ thuật. Những nhà tiên phong về giải tích đã phát hiện ra rằng tất cả các hàm mà họ quen thuộc — sine và cosine, logarit và hàm số mũ — có thể được chuyển đổi thành dòng luân lưu phổ quát của “chuỗi lũy thừa”, một loại phiên bản tăng cường của chuỗi hình học trong đó các hệ số giờ đây có thể cũng thay đổi.
Và khi họ thực hiện những phép chuyển đổi này, họ nhận thấy những sự trùng hợp đáng kinh ngạc. Ví dụ, đây là chuỗi lũy thừa cho các hàm logarith tự nhiên, hàm cosine, sine, và hàm mũ (đừng lo lắng về nguồn gốc của chúng; chỉ cần nhìn vào hình thức bên ngoài của chúng):

Bên cạnh tất cả các dấu chấm than (giai thừa) đầy hoan hỉ và xứng đáng với sự gọn ghẽ của nó, cho ý nghĩa mà nó đại diện, hãy lưu ý rằng chuỗi tính exp(x) xuất hiện đầy trêu ngươi khi gần như là sự kết hợp của hai công thức phía trên nó. Giá như sự xen kẽ của các dấu cộng và dấu trừ trong cos(x) và sin(x) bằng cách nào đó có thể hòa hợp với bộ dấu toàn là dấu cộng của exp(x) thì mọi thứ sẽ khớp với nhau.
Sự trùng hợp đó, và kiểu suy nghĩ viển vông đó, đã đưa Leonhard Euler đến việc khám phá ra một trong những công thức kỳ diệu và sâu rộng nhất trong lịch sử toán học:

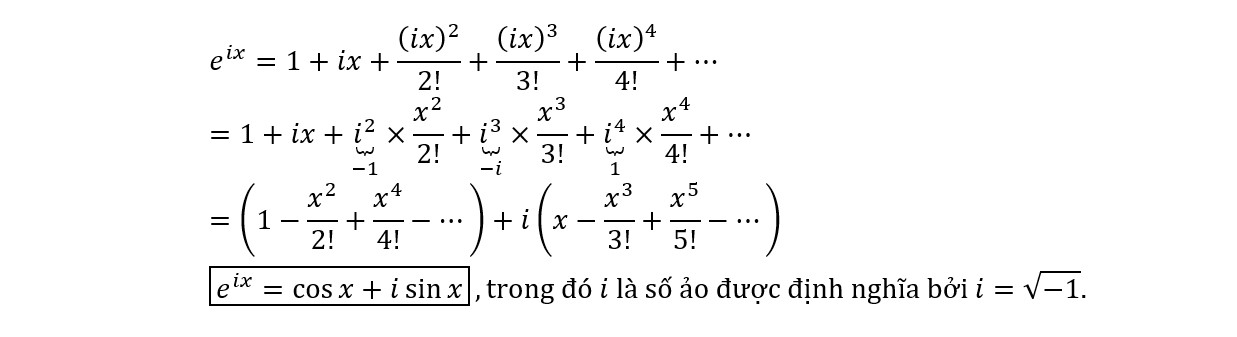
Giả sử các hàm này không thể viết dưới dạng tổng vô hạn thì mối liên hệ ẩn giấu này sẽ không bao giờ được tìm ra, bất kể người ta định nghĩa i là gì đi nữa. Sự “hòa hợp” cần thiết giữa sin(x) và cos(x) chỉ được thực hiện thông qua định nghĩa về số ảo. Điểm cốt lõi để đi tới công thức Euler là giải tỏa được các lũy thừa của i, theo quy tắc i¹=i, i²=–1, i³=–i, i⁴=1, các lũy thừa sau đó tiếp tục lặp đi lặp lại theo thứ tự như vậy.

Công thức của Euler thể hiện một sự kết nối mãnh liệt. Nó cả quyết rằng sine và cosine, hiện thân của chu kỳ và sóng, là những họ hàng bí mật của hàm số mũ, hiện thân của sự tăng trưởng và suy giảm — nhưng chỉ khi chúng ta xem xét việc nâng số e (xấp xỉ 2.718) lên một lũy thừa ảo (bất kể điều đó có nghĩa là gì). Công thức của Euler, được sinh ra trực tiếp bởi chuỗi vô hạn, giờ đây không thể thiếu trong kỹ thuật điện tử, cơ học lượng tử và tất cả các ngành kỹ thuật liên quan đến sóng và chu kỳ.
Đến đây, chúng ta có thể thực hiện một bước cuối cùng, đưa chúng ta đến phương trình thường được mô tả là đẹp nhất trong toán học, cho trường hợp đặc biệt của công thức Euler trong đó x = π (radian):

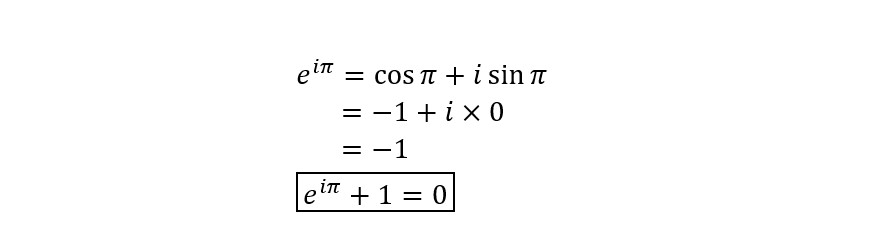
Nó kết nối một vài con số nổi tiếng nhất trong toán học: 0, 1, π, i và e. Mỗi số biểu tượng cho toàn bộ một nhánh của toán học, và theo cách đó, phương trình có thể được coi là một sự hợp lưu huy hoàng, một minh chứng cho sự thống nhất của toán học.
Số 0 đại diện cho hư vô, sự trống rỗng, nhưng nó không phải là sự vắng mặt của con số - đó là số làm cho toàn bộ hệ thống ghi chép số của chúng ta trở nên khả thi. Sau đó có 1, số đơn vị, sự khởi đầu, nền tảng của phép đếm và các con số, và nhìn rộng ra là toàn bộ môn toán ở trường tiểu học. Tiếp theo là số π, biểu tượng của vòng tròn và sự hoàn hảo, nhưng lại có một mặt tối bí ẩn, gợi ra sự vô tận trong khuôn mẫu khó hiểu nơi các chữ số của nó, vô cùng tận, bí hiểm. Ta có i, số ảo, một biểu tượng của đại số, thể hiện những bước nhảy vọt của trí tưởng tượng đầy sáng tạo cho phép con số phá vỡ xiềng xích của độ lớn đơn thuần (bản thân số ảo có dạng chuẩn là z = a+bi, nên khi nhìn vào không thể thấy ngay được độ lớn, hay mô-đun của nó, cho tới khi chúng ta thực hiện phép tính |z|=√(a²+b²)). Và cuối cùng là số e, linh vật của giải tích, một biểu tượng của chuyển động và sự thay đổi.
Khi tôi (tác giả Strogatz) còn là một cậu bé, người bố nói với ông rằng toán học giống như một tòa tháp. Một thứ gì đó được xây dựng tiếp theo bên trên. Phép cộng được xây dựng trên các con số. Phép trừ được xây dựng dựa trên phép cộng (trừ là cộng cho số âm). Và cứ thế tiếp tục, tăng dần qua đại số, hình học, lượng giác và giải tích, cho đến “toán học cao cấp hơn nữa” - cái tên thích hợp cho một dinh cơ cao chót vót.
Nhưng khi tôi học về chuỗi vô hạn, tôi không còn coi toán học là một tòa tháp nữa. Nó cũng không phải là một cái cây theo như một phép ẩn dụ khác. Các bộ phận khác nhau của nó không phải là những nhánh tách ra và đi theo những con đường riêng biệt. Không hề - toán học là một mạng lưới (web). Tất cả các bộ phận của nó kết nối và hỗ trợ lẫn nhau. Không có phần nào của toán học được tách ra khỏi phần còn lại. Đó là một mạng lưới, hơi giống một hệ thống thần kinh - hay tốt hơn là một bộ não.

Theo Steven Strogatz, Quanta Magazine.